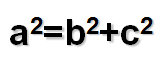1. El triángulo
1.1 Propiedades y tipos de triángulos
Propiedades:1. Un lado de un triángulo es menor que la suma de los otros dos y mayor que su diferencia.
2. La suma de los ángulos interiores de un triángulo es igual a 180°.
3. El valor de un ángulo exterior es igual a la suma de los dos interiores no adyacentes.
1.2 Rectas y puntos notables en el triángulo (http://gaussianos.com/los-centros-del-trianguloincentro-baricentro-circuncentro-y-ortocentro/)
Incentro:
El incentro es el centro de la circunferencia escrita al triángulo, por lo que la distancia a cada uno de sus lados es la misma.Más específicamente, es el punto de encuentro de las bisectrices de cada uno de los ángulos del triángulo, por lo que para constituir gráficamente debemos dibujar las tres bisectrices y limitar el punto de encuentro de las mismas. En la imagen lo vemos:Baricentro
El baricentro de un triángulo es el punto de empalme de las medianas de dicho triángulo. Por ello, para figurar gráficamente el baricentro debemos dibujar las tres medianas y localizar el punto en el que se trozan. Esta es la figura:Circuncentro
El circuncentro de un triángulo es el eje de la circunferencia circunscrita al triángulo, por lo que el trayecto a cada uno de sus vértices es la misma. Por preciso, es el punto de empalme de las mediatrices del triángulo. Por tanto, para representar gráficamente el circuncentro dibujamos las tres mediatrices y localizamos el punto de intersección de las mismas. Puede verse asi:Ortocentro
El ortocentro de un triángulo es el punto de intersección de las tres alturas del triángulo (siendo una altura el segmento que parte de un vértice y es perpendicular al lado opuesto a dicho vértice).1.3 El teorema de Pitágoras
El teorema de Pitágoras se basa en que la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.
1.3.1 Demostración 3D
Matemáticamente se puede enunciar con la siguiente ecuación:
Esta ecuación expresa que el área de un cuadrado de lado “a” es igual a la suma de las áreas de dos cuadrados, uno de lado “b” y otro de lado “c”. Si denominamos “a” a la hipotenusa (lado más largo) de un triángulo rectángulo y “b” y “c” a los catetos, gráficamente se puede representar con la siguiente figura.
1.4 El teorema de Tales (vídeo: Les Luthiers - Teorema De Thales https://www.youtube.com/watch?v=UbalEyegXbQ), triángulos semejantes. ¿Cómo calcular la altura de un árbol a partir de su sombra?
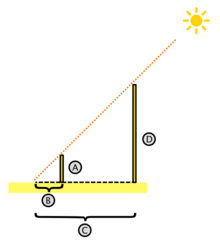
Tales descubrió el teorema mientras investigaba la condición de paralelismo entre dos rectas. De hecho, el primer teorema de Tales puede enunciarse como que la igualdad de los cocientes de los lados de dos triángulos no es condición suficiente de paralelismo. Sin embargo, la principal aplicación del teorema, y la razón de su fama, se deriva del establecimiento de la condición de semejanza de triángulos, a raíz de la cual se obtiene el siguiente corolario.
1.4 El teorema de Tales (vídeo: Les Luthiers - Teorema De Thales https://www.youtube.com/watch?v=UbalEyegXbQ), triángulos semejantes. ¿Cómo calcular la altura de un árbol a partir de su sombra?
Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtiene un triángulo que es semejante al triángulo dado.

Tales descubrió el teorema mientras investigaba la condición de paralelismo entre dos rectas. De hecho, el primer teorema de Tales puede enunciarse como que la igualdad de los cocientes de los lados de dos triángulos no es condición suficiente de paralelismo. Sin embargo, la principal aplicación del teorema, y la razón de su fama, se deriva del establecimiento de la condición de semejanza de triángulos, a raíz de la cual se obtiene el siguiente corolario.
2. Lugares geométricos
2.1 ¿Qué es un lugar geométrico?
Conjunto de puntos que satisfacen determinadas condiciones o propiedades geométricas.2.2 La mediatriz y la bisectriz
MEDIATRIZ: Es la recta perpendicular a un segmento que se traza en su punto medio.BISETRIZ: Es la Semirrecta que parte del vértice de un ángulo y lo divide en dos partes iguales.
2.3 Las cónicas
2.3.1 ¿Qué es una cónica?
Del cono o relacionado con este cuerpo geométrico. También la completan con una ecuación de segundo grado: Bx^2 + Cy^2 + Dxy + Fx + Gy + H=0
2.3.2 La circunferencia
La circunferencia es una linea curva cerrada cuyos puntos están todos a la misma distancia de un punto fijo.Los elementos de la circunferencia son:
- Centro de la circunferencia: el centro es el punto del que equidistan todos los puntos de la circunferencia.
- Radio de la circunferencia: el radio es el segmento que une el centro de la circunferencia con un punto cualquiera de la misma.
- Diámetro: es una cuerda que pasa por el centro de la circunferencia.
- Arco: un arco es cada una de las partes en que una cuerda divide a la circunferencia.
- Semicircunferencia: una semicircunferencia es cada uno de los puntos iguales que abarca el diámetro.
2.3.3 La elipse
Lugar geométrico de los puntos tales que la suma de sus distancias a dos puntos fijos, llamados focos, es una constante.Se llaman vértices de la elipse a los puntos donde ésta corta a sus ejes. El punto medio de los dos focos se llama centro de la elipse y la distancia entre ellos se llama distancia focal.
La línea que une los dos focos se llama eje principal de la elipse y la mediatriz de los mismos eje secundario.
La ecuación de un elipse es x2/a2 + y2/b2 = 0